La determinación del tiempo de fabricación de un elemento en una línea de producción es clave para la optimización de los procesos asociados. Pero, ¿cómo puede calcularse? A continuación, un ejemplo práctico y técnico a través del uso y explotación de datos.

El tiempo de fabricación de un elemento en una línea de producción es, debido a la naturaleza propia del proceso, un valor que no debe variar demasiado en el tiempo. Sólo debe verse afectado de manera significativa por la aparición de alguna anomalía. Esto lo convierte en un dato idóneo para ser estudiado y analizado como una serie temporal.

Se llevará a cabo un análisis de los tiempos de fabricación de un elemento haciendo uso de modelos de autorregresión. Se empleará concretamente la metodología Box-Jenkins, considerando los siguientes bloques:

• Estudio de la estructura de la serie, para determinar si se trata de una serie estacionaria, además de chequear la existencia de outliers.
• Búsqueda de los modelos y parámetros que mejor ajusten la serie, estudiando el ajuste de los modelos ARMA o ARIMA según corresponda y estimando los valores más apropiados para sus parámetros.
• Validación del modelo seleccionado, llevando a cabo un análisis sobre el ruido blanco explicado por el modelo.
• Predicción de valores futuros, haciendo uso del modelo seleccionado, así como la detección de valores outliers.

Estudio de la estructura de la serie

La serie está compuesta por un conjunto de observaciones ordenadas de la variable timesheet_incurred, que representa el tiempo de fabricación, en segundos, que se ha consumido en la ejecución de una determinada operación sobre un elemento.

Con una simple descriptiva se observa una gran amplitud en la distribución de los valores, sobre todo teniendo en cuenta la naturaleza de los mismos.

Búsqueda de los modelos y parámetros

Existen métodos para la estimación de los parámetros del modelo ARIMA basados en la aplicación de algunos tests, pero quizás el más extendido y fácil de usar es el que consiste en calcular y minimizar el error cuadrático medio obtenido de diferentes combinaciones de los parámetros p, q y d del modelo.

En nuestro ejemplo, probando diferentes valores, se obtiene que la combinación con menor MSE es (4,0,20).

Validación del modelo

Para comprobar la validez del modelo se lleva a cabo el análisis de los residuos para determinar si se trata de ruido blanco.

En primer lugar se aplica un test de normalidad sobre los residuos, del cual se desprende que se rechaza la hipótesis de que sigan una distribución normal. Esto es indicativo de que no todo el comportamiento de la serie queda explicado por el modelo. Esto puede ser debido a que la serie sufre muchas anomalías, aunque existe correlación entre los valores.

En segundo lugar, se aplica el test de Durbin-Watson para contrastar la existencia de correlación en los residuos del modelo. El resultado es un valor muy cercano a 2, lo cual indica la NO existencia de correlación en los residuos, por lo que damos el modelo como válido.

Predicción de valores futuros

Haciendo uso del modelo seleccionado se pueden hacer predicciones para los valores próximos de la serie, tal como se observa en el siguiente gráfico.

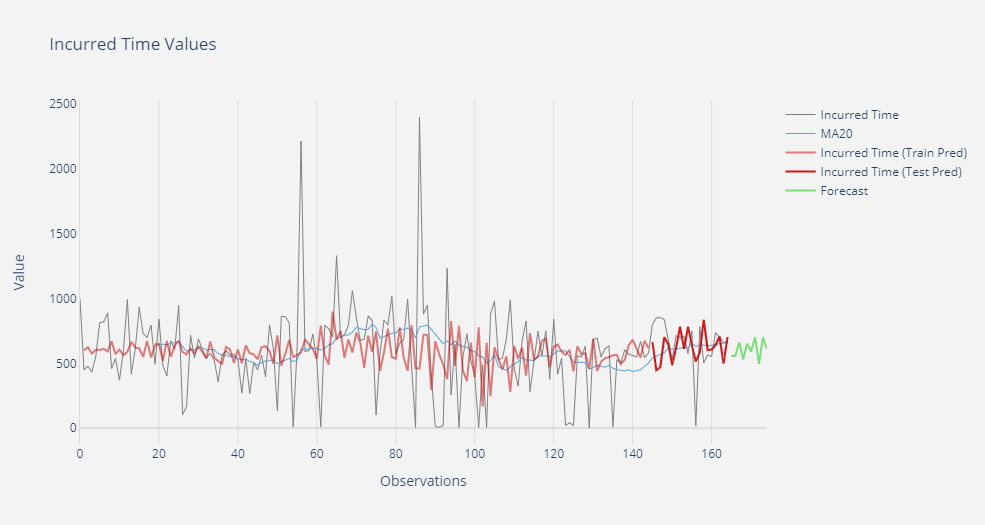
Pero otro beneficio importante de este tipo de análisis sobre una serie temporal es que se puede usar para la detección de anomalías. Haciendo una simple normalización de la serie, se observan outliers dependiendo de la desviación estándar móvil.

Sin embargo, estudiando la desviación entre el valor observado y el valor predicho por el modelo, se pueden detectar anomalías de una manera más sensible que el método anterior. El siguiente gráfico señala anomalías detectadas en aquellos valores cuya desviación con respecto a lo estimado supera la desviación estándar móvil para dicho punto.